Machine Learning Programming Workshop

1.2 Intuition for Machine Learning (Part 1)

Prepared By: Cheong Shiu Hong (FTFNCE)


Contents


In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


Linear Algebra

What is Linear Algebra?

For us, Linear Algebra will only be the use of Vectors and Matrices to represent Data


1) Vectors

return to top

Think of Vectors as storing values in a list

2 Item Vector

$ \vec{a} = \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right] $

5 Item Vector

$ \vec{a} = \left[ {\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5\end{array} } \right] $


1.0 Quick Introduction/Refresher on NumPy

return to top

This is a normal Python List:

In [2]:
a_list = [1, 2, 3] # This is a Python List

We can create a NumPy Array using numpy.array() <-- where the input is a list

In [3]:
a = np.array(a_list) # This is a NumPy Array with a Python List as the Input
In [4]:
b = np.array([1, 2, 3]) # We can directly put the list as the input as well


Notice that when we print a NumPy array, it does not show the comma seperators, as compared to a list

In [5]:
# Print Python List
print(a_list)

[1, 2, 3]
In [6]:
# Print NumPy Array 
print(a)

[1 2 3]
In [7]:
# Print NumPy Array 
print(b) 

[1 2 3]

And when we are too lazy to print them, the outputs look different

In [8]:
a_list # Looks exactly the same as when we printed the Python List
Out[8]:
[1, 2, 3]
In [9]:
a # Wrapped with "array()"
Out[9]:
array([1, 2, 3])


Python Lists are not suitable for Numerical Operations as shown here:

In [10]:
# Python List Multiplied
a_list * 2
Out[10]:
[1, 2, 3, 1, 2, 3]
In [11]:
a_list + 2

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-11-02b9e2681e45> in <module>
----> 1 a_list + 2

TypeError: can only concatenate list (not "int") to list


Arange Function

In [12]:
x = np.arange(start=0, stop=10, step=2)
print(x)

[0 2 4 6 8]

Linspace Function

In [13]:
x = np.linspace(start=0, stop=10, num=5)
print(x)

[ 0.   2.5  5.   7.5 10. ]

Random Numbers (Useful for Monte-Carlo Simulations)

In [14]:
random_number = np.random.normal(loc=10, scale=5) # Mean = 10, Std = 5
print(random_number)

11.317773962493996
In [15]:
random_numbers = np.random.normal(loc=10, scale=5, size=(3,2))
print(random_numbers)

[[10.59898706 16.43157534]
 [10.46388898  9.96613283]
 [17.45742108 13.22887167]]
In [16]:
random_numbers = np.random.randn(3, 2) # Shape of Matrix (Array) Generated from the Standard Normal Distribution
print(random_numbers)

[[-0.1626074   0.31855505]
 [-1.6269628  -1.09416509]
 [ 0.35545624  1.12959288]]
In [17]:
random_numbers = 10 + np.random.randn(3, 2) * 5 # Manually Shifting the Mean, and Scaling the Standard Deviation
print(random_numbers)

[[ 2.13292476  8.92026878]
 [14.579544   15.42312814]
 [12.7183639  10.50124078]]

Manually Shifting and Scaling Distributions for each Column

In [18]:
random_numbers = np.random.randn(3,2)
random_numbers[:,0] = 10 + random_numbers[:,0] * 5 # First Column with Mean = 10, Std = 5
random_numbers[:,1] = 50 + random_numbers[:,1] * 10 # Second Column with Mean = 50, Std = 10
print(random_numbers)

[[11.50909305 49.95876646]
 [16.39788216 47.6661138 ]
 [15.95814151 59.84214946]]

Normal Distribution

In [19]:
x = 10 + np.random.randn(10000) * 10 # Generate 1000 Normally Distribued Numbers in an Array

print('Mean: {:.2f} | Standard Deviation: {:.2f}'.format(x.mean(), x.std())) # Verify the Mean and Standard Deviation

Mean: 10.05 | Standard Deviation: 10.07
In [20]:
plt.hist(x, bins=20, color='green')
plt.show();

Uniform Distribution

In [21]:
x = np.random.uniform(low=10, high=20, size=10000) # Generate 1000 Uniformly Distributed Numbers in an Array

print('Mean: {:.2f} | Standard Deviation: {:.2f}'.format(x.mean(), x.std())) # Verify the Mean and Standard Deviation

Mean: 15.02 | Standard Deviation: 2.89
In [22]:
plt.hist(x, bins=20, color='green')
plt.show();

Transpose Method

In [23]:
print(random_numbers) # 3x2 Matrix

[[11.50909305 49.95876646]
 [16.39788216 47.6661138 ]
 [15.95814151 59.84214946]]
In [24]:
print(random_numbers.T) # 2x3 Matrix

[[11.50909305 16.39788216 15.95814151]
 [49.95876646 47.6661138  59.84214946]]


1.1 Scalar Operations on Vectors

return to top

Let's think of Vector $\vec{a}$ as Tom having 1 Apple and Harry having 2 Apples.

Vector $\vec{a}$

$ \vec{a} = \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right] $

In [25]:
a = np.array([1, 2])


Addition

If I gave both Tom and Harry 2 Apples:

$ 2 + \vec{a}$

$= 2 + \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right]$

$= \left[ {\begin{array}{c} 3 \\ 4\end{array} } \right]$

In [26]:
2 + a
Out[26]:
array([3, 4])


Multiplication

If both Tom and Harry Doubled their Apples:

$ 2 \times \vec{a}$

$= 2 \times \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right]$

$= \left[ {\begin{array}{c} 2 \\ 4\end{array} } \right]$

In [27]:
2 * a
Out[27]:
array([2, 4])


Notice that for Scalar Operations, order does NOT Matter

In [28]:
a + 2
Out[28]:
array([3, 4])
In [29]:
a * 2
Out[29]:
array([2, 4])


1.2 Element-Wise Operations of Vectors

return to top

Let's think of Vector $\vec{a}$ as Tom earning 1 Dollar/Day and Harry earning 2 Dollars/Day.

Vector $\vec{a}$ and Vector $\vec{b}$

$ \vec{a} = \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right] $

$ \vec{b} = \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right] $

In [30]:
a = np.array([1, 2])
b = np.array([5, 6])


Addition

If I gave Tom 5 Dollars and Harry 6 Dollars:

$\vec{a} + \vec{b}$

$= \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right] + \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right]$

$= \left[ {\begin{array}{c} 6 \\ 8\end{array} } \right] $

In [31]:
a + b
Out[31]:
array([6, 8])


Multiplication

If Tom works 5 Days a Week and Harry Works 6 Days a Week:

$\vec{a} \times \vec{b}$


$= \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right] \times \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right]$

$= \left[ {\begin{array}{c} 5 \\ 12\end{array} } \right] $

In [32]:
a * b
Out[32]:
array([ 5, 12])


Notice that for Element-Wise Operations, order does NOT Matter also

In [33]:
b + a
Out[33]:
array([6, 8])
In [34]:
b * a
Out[34]:
array([ 5, 12])


1.3 Dot Product of Vectors

return to top

For Vectors, the Dot Product is pretty much Multiplying each Pair and summing the Product Together

How Much Money will Both Tom and Harry have after the week?

$\vec{a} . \vec{b}$


$= \left[ {\begin{array}{c} 1 \\ 2\end{array} } \right] . \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right]$

$= (1 \times 5) + (2 \times 6)$

$= 5 + 12$

$= 17$

In [35]:
np.dot(a, b)
Out[35]:
17

More formally, the Dot Product is the product of the length of a Vector multiplied by the length of the other Vector projected onto itself.

$\vec{a}.\vec{b}$ = $||\vec{a}||$ . $||\vec{b}||$ . $cos(\theta)$, where $|\vec{a}|$ is the size (length) of $\vec{a}$ and $\theta$ is the angle between $\vec{a}$ and $\vec{b}$.



Fun Fact: The Dot Product of a Vector with itself is pretty much the squared size (length) of the Vector, since:
$\theta = 0$ (Angle between a Vector and itself is $0^o$) cos$(\theta) = 1$ (Cosine of 0 is 1) $\therefore \vec{a}.\vec{a}$ $= ||\vec{a}|| . ||\vec{a}|| . cos(\theta)$ $= ||\vec{a}|| . ||\vec{a}||$ $= ||\vec{a}||^2$

With the same logic, if two Vectors are Orthogonal ($90^o$ from each other), the Dot Product will be 0, since cos(90) = 0

And for Vectors Pointing in the Opposite Direction, the Dot Product will be Negative since cos$(\theta)$ < 0 for ($90^o$ < $\theta$ <= $180^o$)


Click here if you're interested to learn more


2) Matrices

return to top

Think of Matrices as Multiple Vectors in another Vector

In [36]:
A = np.array([[1,2,3],
              [4,5,6]])

B = np.array([[9,8,7,6],
              [8,7,6,5],
              [7,6,5,4]])
In [37]:
print('Shape of A:\n', A.shape)
print('Shape of B:\n', B.shape)

Shape of A:
 (2, 3)
Shape of B:
 (3, 4)


2.1 Scalar Operations on Matrices

return to top

In [38]:
A
Out[38]:
array([[1, 2, 3],
       [4, 5, 6]])


Adding/Multiplying a Number with Matrices

Scalar will be broadcasted and operated on every value in the Matrix

In [39]:
10 + A
Out[39]:
array([[11, 12, 13],
       [14, 15, 16]])
In [40]:
10 * A
Out[40]:
array([[10, 20, 30],
       [40, 50, 60]])


2.2 Element-Wise Operations of Matrices

return to top

In [41]:
A
Out[41]:
array([[1, 2, 3],
       [4, 5, 6]])
In [42]:
B
Out[42]:
array([[9, 8, 7, 6],
       [8, 7, 6, 5],
       [7, 6, 5, 4]])


Adding/Multiplying Different Shaped Matrices Together?

In [43]:
A + B

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-43-151064de832d> in <module>
----> 1 A + B

ValueError: operands could not be broadcast together with shapes (2,3) (3,4)
In [44]:
B + A

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-44-b1a194f9b6dc> in <module>
----> 1 B + A

ValueError: operands could not be broadcast together with shapes (3,4) (2,3)
In [45]:
A * B

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-45-a4cedde81ed0> in <module>
----> 1 A * B

ValueError: operands could not be broadcast together with shapes (2,3) (3,4)
In [46]:
B * A

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-46-36ca14b77ca1> in <module>
----> 1 B * A

ValueError: operands could not be broadcast together with shapes (3,4) (2,3)

NOTE: Matrices have to be of the SAME SHAPE for Element-Wise Operations!

In [47]:
A + A
Out[47]:
array([[ 2,  4,  6],
       [ 8, 10, 12]])
In [48]:
B + B
Out[48]:
array([[18, 16, 14, 12],
       [16, 14, 12, 10],
       [14, 12, 10,  8]])
In [49]:
A * A
Out[49]:
array([[ 1,  4,  9],
       [16, 25, 36]])
In [50]:
B * B
Out[50]:
array([[81, 64, 49, 36],
       [64, 49, 36, 25],
       [49, 36, 25, 16]])


2.3 Dot Product of Matrices

return to top

Intuition Behind the Operation:

There are 2 Fruit Stalls, each selling fruits at different prices:

Stall 1 sells Apple for 1 Dollar, Banana for 2 Dollar, Carrot for 3 Dollar

Stall 2 sells Apple for 3 Dollar, Banana for 4 Dollar, Carrot for 5 Dollar


$A = \left[ {\begin{array}{c} 1 & 2 & 3 \\ 4 & 5 & 6\end{array} } \right]$

The number of Days of Data recorded is 4 (A.K.A 4 Samples)

E.g. I bought 9 Apples, 8 Bananas, 7 Carrots on Day 1,

and I bought 8 Apples, 7 Bananas, 6 Carrots on Day 2...


$B = \left[ {\begin{array}{c} 9 & 8 & 7 & 6 \\ 8 & 7 & 6 & 5 \\ 7 & 6 & 5 & 4\end{array} } \right]$


Taking the Dot Product of (2 Stalls x 3 Fruits) and (3 Fruits x 4 Days) can be interpreted as:

Finding the amount spent at Each Stall, on Each Day.

Output: (2 Stalls, 4 Days)

Notice (3 Fruits) is not in the Output, as that is our "Inner Dimension" or the Dimension that we are Summing over.

$A.B = \left[ {\begin{array}{c} 1 & 2 & 3 \\ 4 & 5 & 6\end{array} } \right] . \left[ {\begin{array}{c} 9 & 8 & 7 & 6 \\ 8 & 7 & 6 & 5 \\ 7 & 6 & 5 & 4\end{array} } \right]$

$= \left[ {\begin{array}{c} (1 \times 9) + (2 \times 8) + (3 \times 7) & ... \\ (4 \times 9) + (5 \times 8) + (6 \times 7) & ...\end{array} } \right]$


$= \left[ {\begin{array}{c} 46 & 40 & 34 & 28 \\ 118 & 103 & 88 & 73 \end{array} } \right]$


We can only take the Dot Product of a (M x N) matrix, with a (N x O) matrix, where the Inner Dimensions Match

$\mathbb{R}^{M \times N} . \mathbb{R}^{N \times O} = \mathbb{R}^{M \times O}$

Dot Product of (M x N) matrix and (N x O) matrix gives us (M x O) Matrix

In [51]:
print('Matrix A:'); print(A); print('Shape:', A.shape)

Matrix A:
[[1 2 3]
 [4 5 6]]
Shape: (2, 3)
In [52]:
print('Matrix B:'); print(B); print('Shape:', B.shape)

Matrix B:
[[9 8 7 6]
 [8 7 6 5]
 [7 6 5 4]]
Shape: (3, 4)

Dot Product of (2 x 3) Matrix and (3 x 4) Matrix gives us (2 x 4) Matrix

In [53]:
np.dot(A, B)
Out[53]:
array([[ 46,  40,  34,  28],
       [118, 103,  88,  73]])
In [54]:
np.dot(A, B).shape
Out[54]:
(2, 4)


$\mathbb{R}^{N \times O} . \mathbb{R}^{M \times N} = ERROR$

Dot Product of (N x O) matrix and (M x N) matrix gives us Error!

Inner Dimensions Do Not Match!

In [55]:
np.dot(B, A)

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-55-831079463ca7> in <module>
----> 1 np.dot(B, A)

ValueError: shapes (3,4) and (2,3) not aligned: 4 (dim 1) != 2 (dim 0)


2.4 Row Vectors vs Column Vectors

return to top

Which is a Row Vector and which is a Column Vector?

$\vec{a} = \left[ {\begin{array}{c} 1 & 2\end{array} } \right]$

$\vec{b} = \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right]$

In [56]:
a = np.array([1,2])

b = np.array([5,
              6])

print('Vector a:\n', a)
print('Vector b:\n', b)

Vector a:
 [1 2]
Vector b:
 [5 6]
In [57]:
print('Shape of a:\n', a.shape)
print('Shape of b:\n', b.shape)

Shape of a:
 (2,)
Shape of b:
 (2,)


How do we Differentiate between a Row Vector vs a Column Vector in NumPy?

$\vec{a} = \left[ {\begin{array}{c} 1 & 2\end{array} } \right]$

$\vec{b} = \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right]$

Think of Row Vectors as a 1-Row, N-Column Matrix (1 x N)

Think of Column Vectors as a N-Row, 1-Column Matrix (N x 1)

In [58]:
a = np.array([[1, 2]])

b = np.array([[5], 
              [6]])

print('Vector a:\n', a)
print('Vector b:\n', b)

Vector a:
 [[1 2]]
Vector b:
 [[5]
 [6]]
In [59]:
print('Shape of a:\n', a.shape)
print('Shape of b:\n', b.shape)

Shape of a:
 (1, 2)
Shape of b:
 (2, 1)


Dot Product of Row Vector with Column Vector

$\left[ {\begin{array}{c} 1 & 2\end{array} } \right] . \left[ {\begin{array}{c} 5 \\ 6\end{array} } \right]$

In [60]:
np.dot(a, b)
Out[60]:
array([[17]])


Dot Product of Column Vector with Row Vector

$\left[ {\begin{array}{c} 5 \\ 6\end{array} } \right] . \left[ {\begin{array}{c} 1 & 2\end{array} } \right]$

In [61]:
np.dot(b, a)
Out[61]:
array([[ 5, 10],
       [ 6, 12]])


Practice Questions:

return to top

Let's Try Some Practice Questions:

Question 1

Calculate the Following:

$3 \times \left[ {\begin{array}{c} 2 & 7 \\ 1 & 5\end{array} } \right]$


Question 2

Calculate the Dot Product of the Following:

$\left[ {\begin{array}{c} 4 & 3\end{array} } \right] . \left[ {\begin{array}{c} 2 \\ 5\end{array} } \right]$


Question 3

Calculate the Dot Product of the Following:

$\left[ {\begin{array}{c} 2 & 6 & -1 \\ -3 & 4 & 3 \end{array} } \right] . \left[ {\begin{array}{c} 2 & 4 \\ 5 & -2 \\ 3 & -1 \end{array} } \right]$


Question 4

Calculate the Dot Product of the Following:

$\left[ {\begin{array}{c} 2 & 6 & -1 & 5 & 7\\ -3 & 4 & 3 & 2 & -7 \\ -1 & 2 & -2 & -5 & 4 \\ 3 & 2 & 8 & -4 & 3\end{array} } \right] . \left[ {\begin{array}{c} 2 & 4 & 5\\ 5 & -2 & 1 \\ 3 & -1 & -7 \\ -2 & -4 & -4 \\ 4 & 6 & 1 \end{array} } \right]$

JK. We should use NumPy for this:

In [62]:
a = np.array([[ 2, 6, -1,  5,  7],
              [-3, 4,  3,  2, -7],
              [-1, 2, -2, -5,  4],
              [ 3, 2,  8, -4,  3]])

b = np.array([[ 2,  4,  5],
              [ 5, -2,  1],
              [ 3, -1, -7],
              [-2, -4, -4],
              [ 4,  6,  1]])

np.dot(a, b)
Out[62]:
array([[ 49,  19,  10],
       [ -9, -73, -47],
       [ 28,  38,  35],
       [ 60,  34, -20]])


Notice that when we (Humans) vectorize information, we calculate each item sequentially, so it seems like there are no benefits to this

However, computers benefit greatly from vectorization:

In [63]:
# Create 1,000,000 Sized Arrays
a = np.random.randn(1000000)
b = np.random.randn(1000000)

print(a.shape, b.shape)

(1000000,) (1000000,)
In [64]:
%%time

# Explicit For Loops
c = 0
for i in range(len(a)):
    c += a[i] * b[i]
print(c)

-738.5690346418623
Wall time: 506 ms
In [65]:
%%time

# Element-Wise Multiplication, then Summing them together
c = sum(a * b)
print(c)

-738.5690346418623
Wall time: 165 ms
In [66]:
%%time

# Matrix Multiplication
c = a @ b
print(c)

-738.5690346418631
Wall time: 0 ns
In [67]:
%%time

# Dot Product
c = np.dot(a, b)
print(c)

-738.5690346418631
Wall time: 1.01 ms

It seems like utilizing NumPy's Dot Product Operation can be ~14x Faster than Explicit For-Loops!

In fact it can be ~1000x Faster when dealing with Larger Arrays as seen in the 100,000,000 sized calculations below

Also, when we utilize Machine Learning Libraries like PyTorch and Tensorflow that utilizes GPU power, 43s can become 4ms

NumPy

PyTorch

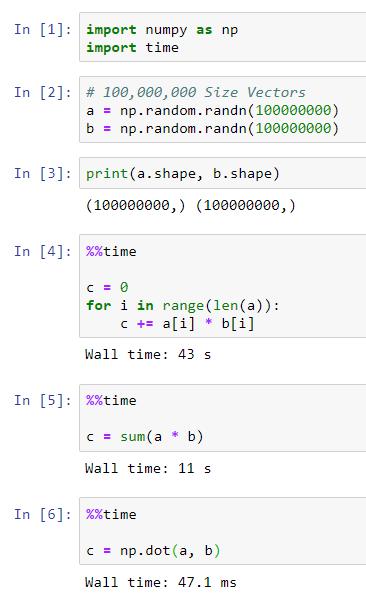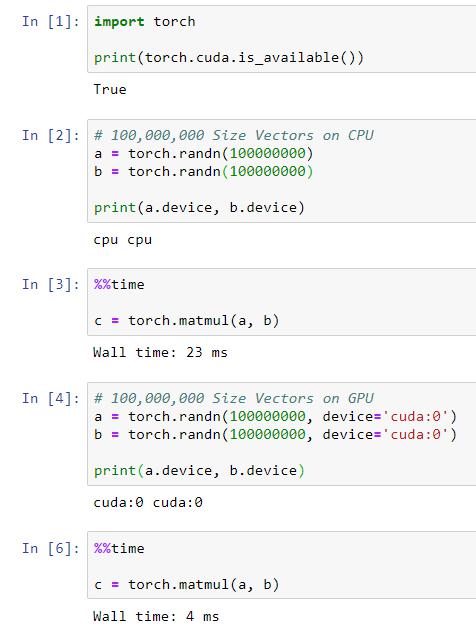The GPU with PyTorch was done on a Desktop Computer with an nVidia GPU (We won't be able to do that with Laptop Integrated Graphics unless you're a hardcore gamer and you have your dedicated graphics properly set up).

Or, we could use Cloud Computing Services).


Example 1:

return to top

2 Apples + 1 Banana will Cost $13

3 Apples + 2 Banana will Cost $22

Vectorize the Information as:

$\left[ {\begin{array}{c} 2 & 1 \\ 3 & 2\end{array} } \right] . \left[ {\begin{array}{c} A \\ B\end{array} } \right] = \left[ {\begin{array}{c} 13 \\ 22\end{array} } \right]$

Dot Product would give us:

$\left[ {\begin{array}{c} 2A + 1B \\ 3A + 2B\end{array} } \right] = \left[ {\begin{array}{c} 13 \\ 22\end{array} } \right]$

Think of Rows as Samples, Columns as Variables for Each Item {A, B}

Solving {A, B} is not the Point here, the Representation of Data by Vectorization is the Point.

A = 4

B = 5

Solving with Linear Algebra

In [68]:
units = np.array([[2,1], [3,2]])
cost = np.array([13,22])
In [69]:
np.linalg.inv(units) @ cost
Out[69]:
array([4., 5.])


Example 2:

return to top

2 Apples + 1 Banana will Cost $12

3 Apples + 2 Banana will Cost $19

New Variable: Ordering Cost of $O/Purchase

O = ?

Vectorize the Information as:

$\left[ {\begin{array}{c} 2 & 1 \\ 3 & 2\end{array} } \right] . \left[ {\begin{array}{c} A \\ B\end{array} } \right] + O = \left[ {\begin{array}{c} 12 \\ 19\end{array} } \right]$

Dot Product would give us:

$\left[ {\begin{array}{c} 2A + 1B \\ 3A + 2B\end{array} } \right] + O = \left[ {\begin{array}{c} 12 \\ 19\end{array} } \right]$

Broadcast O:

$\left[ {\begin{array}{c} 2A + 1B + O\\ 3A + 2B + O\end{array} } \right] = \left[ {\begin{array}{c} 12 \\ 19\end{array} } \right]$

Think of Rows as Samples, Columns as Variables for Each Item {A, B}

Again, Solving {A, B, O} is not the Point here, the Representation of Data by Vectorization is the Point.

A = 3

B = 4

O = 2

Note that we can always re-write as:

$\left[ {\begin{array}{c} 2 & 1\\ 3 & 2\end{array} } \right] . \left[ {\begin{array}{c} A \\ B\end{array} } \right] = \left[ {\begin{array}{c} 12-O \\ 19-O\end{array} } \right]$

or

$\left[ {\begin{array}{c} 2 & 1 & 1\\ 3 & 2 & 1\end{array} } \right] . \left[ {\begin{array}{c} A \\ B\\ O \end{array} } \right] = \left[ {\begin{array}{c} 12 \\ 19\end{array} } \right]$


Example 3:

return to top

2 Apples + 1 Banana will Cost $13

3 Apples + 2 Banana will Cost $18

New Variable: Ordering Cost of $2/Purchase

O = 2

Vectorize the Information as:

$\left[ {\begin{array}{c} 2 & 1 \\ 3 & 2\end{array} } \right] . \left[ {\begin{array}{c} A \\ B\end{array} } \right] + 2 = \left[ {\begin{array}{c} 13 \\ 18\end{array} } \right]$

Dot Product would give us:

$\left[ {\begin{array}{c} 2A + 1B \\ 3A + 2B\end{array} } \right] + 2 = \left[ {\begin{array}{c} 13 \\ 18\end{array} } \right]$

Broadcast 2:

$\left[ {\begin{array}{c} 2A + 1B + 2\\ 3A + 2B + 2\end{array} } \right] = \left[ {\begin{array}{c} 13 \\ 18\end{array} } \right]$

Now we shift our focus to Finding the Best Estimate of A and B, to minimize the Error in Predicted Cost

For Instance:

A = 3

B = 4

$Predicted = \left[ {\begin{array}{c} 2 & 1 \\ 3 & 2\end{array} } \right] . \left[ {\begin{array}{c} 3 \\ 4\end{array} } \right] + 2$

$= \left[ {\begin{array}{c} 2\times3 + 1\times4 \\ 3\times3 + 2\times4\end{array} } \right] + 2$

$= \left[ {\begin{array}{c} 6 + 4\\ 9 + 8\end{array} } \right] + 2$

$= \left[ {\begin{array}{c} 10\\ 17\end{array} } \right] + 2$

$= \left[ {\begin{array}{c} 12 \\ 19\end{array} } \right]$

$Error = Prediction - Actual$

$Error = \left[ {\begin{array}{c} 12 \\ 19\end{array} } \right] - \left[ {\begin{array}{c} 13 \\ 18\end{array} } \right]$

$= \left[ {\begin{array}{c} -1 \\ 1\end{array} } \right]$

Are there better answers?


To see how we can minimize Error, we will look into Differentiation in the Part 2.


Demonstration of the Use of Linear Algebra in Machine Learning / Data Analysis

In [70]:
prices = pd.read_csv('./sources/prices.csv', index_col=0)
In [71]:
prices.head()
Out[71]:
^DJI ^GSPC ^IXIC ^N225 ^STI ^FTSE
Date
1988-01-05 2031.500000 258.630005 344.100006 21575.279297 879.299988 1789.599976
1988-01-06 2037.800049 258.890015 346.700012 22790.500000 906.000000 1787.099976
1988-01-07 2051.889893 261.070007 349.700012 22792.130859 911.500000 1787.199951
1988-01-11 1945.130005 247.490005 336.200012 22578.429688 849.099976 1760.199951
1988-01-12 1928.550049 245.419998 332.000000 22625.050781 870.500000 1739.199951
In [72]:
returns = prices.pct_change().dropna()
In [73]:
returns.head()
Out[73]:
^DJI ^GSPC ^IXIC ^N225 ^STI ^FTSE
Date
1988-01-06 0.003101 0.001005 0.007556 0.056325 0.030365 -0.001397
1988-01-07 0.006914 0.008421 0.008653 0.000072 0.006071 0.000056
1988-01-11 -0.052030 -0.052017 -0.038605 -0.009376 -0.068459 -0.015107
1988-01-12 -0.008524 -0.008364 -0.012493 0.002065 0.025203 -0.011930
1988-01-13 -0.001981 0.001589 0.002108 -0.013262 -0.019069 -0.003335
In [74]:
returns.describe()
Out[74]:
^DJI ^GSPC ^IXIC ^N225 ^STI ^FTSE
count 5696.000000 5696.000000 5696.000000 5696.000000 5696.000000 5696.000000
mean 0.000534 0.000517 0.000696 0.000146 0.000330 0.000326
std 0.012212 0.012676 0.016322 0.016415 0.014444 0.012733
min -0.083504 -0.090350 -0.111869 -0.115083 -0.143733 -0.097180
25% -0.004861 -0.004930 -0.006482 -0.008044 -0.005957 -0.005836
50% 0.000718 0.000750 0.001299 0.000401 0.000214 0.000568
75% 0.006316 0.006371 0.008246 0.008887 0.006512 0.006594
max 0.111719 0.109862 0.174129 0.141503 0.165564 0.117520

Principal Component Analysis

In [75]:
corr_matrix = returns.corr()
print(corr_matrix)

           ^DJI     ^GSPC     ^IXIC     ^N225      ^STI     ^FTSE
^DJI   1.000000  0.961414  0.778719  0.240502  0.312357  0.568400
^GSPC  0.961414  1.000000  0.865143  0.247373  0.313128  0.581679
^IXIC  0.778719  0.865143  1.000000  0.231036  0.299734  0.503981
^N225  0.240502  0.247373  0.231036  1.000000  0.454051  0.365782
^STI   0.312357  0.313128  0.299734  0.454051  1.000000  0.425637
^FTSE  0.568400  0.581679  0.503981  0.365782  0.425637  1.000000
In [76]:
eigvals, eigvecs = np.linalg.eig(corr_matrix) # Eigen-decomposition of the Correlation Matrix
In [77]:
idx = np.argsort(eigvals)[::-1]
eigvals = eigvals[idx]
eigvecs = eigvecs[:, idx]
var_contri = eigvals / eigvals.sum()
In [78]:
plt.title('Scree Plot', fontsize=16)
plt.plot(var_contri, c='blue')
plt.show();
In [79]:
fig = plt.figure(figsize=(10,4))
plt.title('Principal Components', fontsize=16)
colors = ['blue', 'purple', 'orange']
num = 3
for i in range(3):
    plt.plot(eigvecs[:,i], c=colors[i])
    plt.scatter(returns.columns, eigvecs[:,i], c=colors[i], label='PC{} {:.2f}%'.format(i+1, var_contri[i]*100))
plt.legend()
plt.show();

Monte Carlo Simulations

In [80]:
L = np.linalg.cholesky(returns.cov()) # Cholesky Decomposition of Covariance Matrix
In [81]:
portfolios = np.array([eigvecs[:,i]/eigvecs[:,i].sum() for i in range(len(eigvals))])
In [82]:
n_sims = 10000
z = np.random.randn(n_sims, 252, len(L))
x = z @ L.T + returns.mean().values
sim_rets = ((x+1).prod(axis=1)-1) @ portfolios.T
In [83]:
for i in range(len(portfolios)):
    print(f'Portfolio {i+1}')
    print('Mean Returns: {:.2f}% | Volatility: {:.2f}%'.format(sim_rets[:,i].mean()*100, sim_rets[:,i].std()*100))

Portfolio 1
Mean Returns: 12.45% | Volatility: 19.57%
Portfolio 2
Mean Returns: -5.81% | Volatility: 50.45%
Portfolio 3
Mean Returns: -25.02% | Volatility: 359.57%
Portfolio 4
Mean Returns: 92.96% | Volatility: 355.04%
Portfolio 5
Mean Returns: 97.80% | Volatility: 341.34%
Portfolio 6
Mean Returns: 61.12% | Volatility: 131.29%
In [84]:
plt.title('Returns Distribution') # Returns Distribution of Portfolio 1
plt.hist(sim_rets[:,0], bins=20) 
plt.show();
In [85]:
VAR = np.quantile(sim_rets[:,0], 0.05)
print('{:.2f}%'.format(VAR*100)) # Value at Risk % - 5% Chance to Lose More than:

-16.90%
In [86]:
CVAR = sim_rets[:,0][sim_rets[:,0] < VAR].mean()
print('{:.2f}%'.format(CVAR*100)) # Conditional Value at Risk % - 5% to Lose:

-22.49%




Previous: Next: