Machine Learning Programming Workshop

3.2 Introduction to Neural Networks

Prepared By: Cheong Shiu Hong (FTFNCE)


Contents


In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn as sk
from sklearn import datasets
import time


1) Intuition Behind Neural Networks

return to top

Knowing what Multi-Class Logistic Regression is, we can simply Add Layers for it to be considered a Neural Network:

2-Layer Neural Network (1 Hidden Layer): $(L=2)$

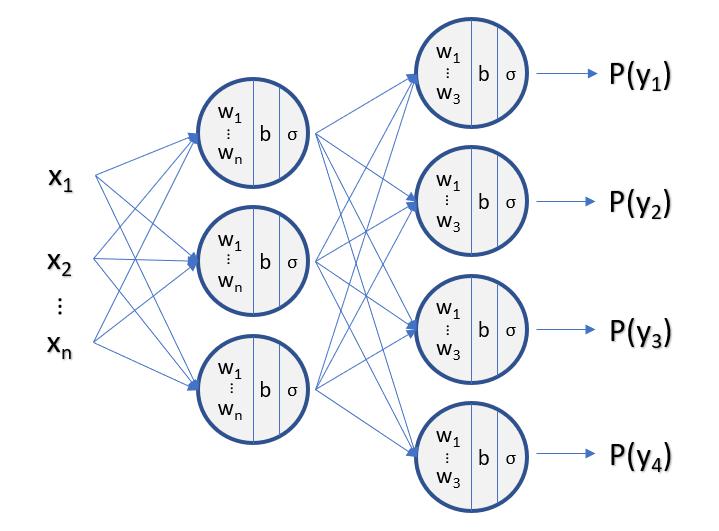
3-Layer Neural Network (2 Hidden Layers): $(L=3)$


2) Forward Pass in Neural Networks

return to top

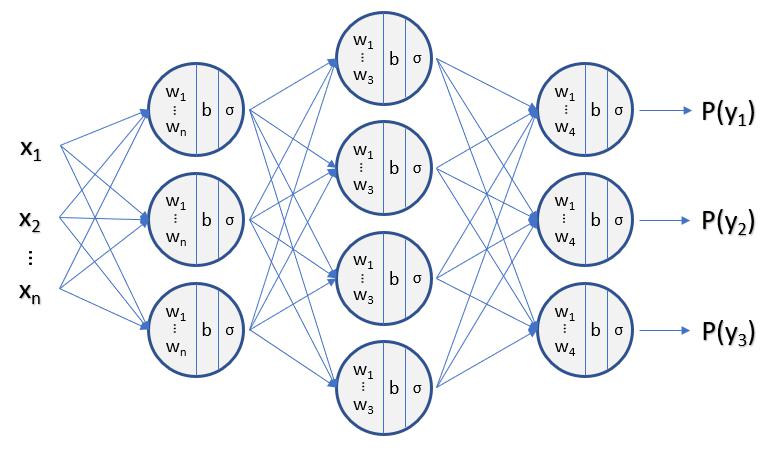
Notation Alert:

$\large A_{<l>}$ indicates that this is $\large A$ (Activated Output) in the $\large l^{th}$ Layer

E.g. $Z_{<2>}$ indicates this is the Pre-Activation Function Output in the Second Layer.

In the First Hidden Layer: $(l=1)$

$Z_{<1>} = W_{<1>}^{T} X + B_{<1>}$

$A_{<1>} = \sigma(Z_{<1>})$, where $\sigma$ is the Chosen Activation Function


In the Second Hidden Layer: $(l=2)$

$Z_{<2>} = W_{<2>}^{T} A_{<1>} + B_{<2>}$

$A_{<2>} = \sigma(Z_{<2>})$, where $\sigma$ is the Chosen Activation Function


In the Final (Output) Layer: $(l=L=3)$

$Z_{<3>} = W_{<3>}^{T} A_{<2>} + B_{<3>}$

$\hat{Y} = \sigma(Z_{<3>})$, where $\sigma$ is the Softmax Activation Function


3) Backpropagation in Neural Networks

return to top

When do we use Dot-Product and Element-Wise Multiplication when calculating Gradients?

In the Final (Output) Layer: $(l=L=3)$

Similar to Multi-Class Logistic Regression, the Gradients of $\hat{Y}$ and $Z_{<3>}$ are:

$\frac{dCost}{d\hat{Y}} = \frac{\hat{Y} - Y}{\hat{Y} (1 - \hat{Y})}$

$\frac{d\hat{Y}}{dZ_{<3>}} = \hat{Y}(1 - \hat{Y})$

Therefore:

$\frac{dCost}{dZ_{<3>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}}$

$= \frac{\hat{Y} - Y}{\hat{Y} (1 - \hat{Y})} \times \hat{Y}(1 - \hat{Y})$

$= \hat{Y} - Y$


Parameters to Update:

$W_{<3>}, B_{<3>}, W_{<2>}, B_{<2>}, W_{<1>}, B_{<1>}$

$\frac{dCost}{dW_{<3>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dW_{<3>}}$

$\frac{dCost}{dB_{<3>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dB_{<3>}}$

$\frac{dCost}{dW_{<2>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}} \times \frac{dA_{<2>}}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dW_{<2>}}$

$\frac{dCost}{dB_{<2>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}} \times \frac{dA_{<2>}}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dB_{<2>}}$

$\frac{dCost}{dW_{<1>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}} \times \frac{dA_{<2>}}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dA_{<1>}} \times \frac{dA_{<1>}}{dZ_{<1>}} \times \frac{dZ_{<1>}}{dW_{<1>}}$

$\frac{dCost}{dB_{<1>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}} \times \frac{dA_{<2>}}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dA_{<1>}} \times \frac{dA_{<1>}}{dZ_{<1>}} \times \frac{dZ_{<1>}}{dB_{<1>}}$


Similar to Multi-Class Logistic Regression, the Gradients of $\hat{Y}$ and $Z_{<3>}$ are:

$\frac{dCost}{d\hat{Y}} = \frac{\hat{Y} - Y}{\hat{Y} (1 - \hat{Y})}$

$\frac{d\hat{Y}}{dZ_{<3>}} = \hat{Y}(1 - \hat{Y})$

Therefore:

$\frac{dCost}{dZ_{<3>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}}$

$= \frac{\hat{Y} - Y}{\hat{Y} (1 - \hat{Y})} \times \hat{Y}(1 - \hat{Y})$

$= \hat{Y} - Y$

The Gradients of the Weights and Biases are:

$\frac{dZ_{<3>}}{dW_{<3>}} = A_{<2>}$

$\frac{dZ_{<3>}}{dB_{<3>}} = 1$

And:

$\frac{dCost}{dW_{<3>}} = \frac{dCost}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dW_{<3>}}$

$\frac{dCost}{dB_{<3>}} = \frac{dCost}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dB_{<3>}}$

Therefore:

$\frac{dCost}{dW_{<3>}} = (\hat{Y} - Y) \times A_{<2>}^{T}$ (n_C, m) x (m, n_H2)

$\frac{dCost}{dW_{<3>}} = (\hat{Y} - Y) A_{<2>}^{T}$ (n_C, n_H2)


$\frac{dCost}{dB_{<3>}} = (\hat{Y} - Y) \times 1$

$\frac{dCost}{dB_{<3>}} = \hat{Y} - Y$


In the Second Hidden Layer: $(l=2)$

The Gradients of $A_{<2>}$ and $Z_{<2>}$ are:

$\frac{dCost}{dA_{<2>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}}$

$\frac{dCost}{dA_{<2>}} = \frac{dCost}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}}$

$\frac{dCost}{dA_{<2>}} = (\hat{Y} - Y)^{T} \times W_{<3>}$

$\frac{dCost}{dA_{<2>}} = (\hat{Y} - Y)^{T} W_{<3>}$

$\frac{dA_{<2>}}{dZ_{<2>}} = A_{<2>}(1 - A_{<2>})$

Therefore:

$\frac{dCost}{dZ_{<2>}} = \frac{dCost}{dA_{<2>}} \times \frac{dA_{<2>}}{dZ_{<2>}}$

$= (\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})$ (Element-Wise)

The Gradients of the Weights and Biases are:

$\frac{dZ_{<2>}}{dW_{<2>}} = A_{<1>}$

$\frac{dZ_{<2>}}{dB_{<2>}} = 1$

And:

$\frac{dCost}{dW_{<2>}} = \frac{dCost}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dW_{<2>}}$

$\frac{dCost}{dB_{<2>}} = \frac{dCost}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dB_{<2>}}$

Therefore:

$\frac{dCost}{dW_{<2>}} = [(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})] \times A_{<1>}^{T}$ (n_H2, m) x (m, n_H1)

$\frac{dCost}{dW_{<2>}} = [(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})] A_{<1>}^{T}$ (n_H2, n_H1)


$\frac{dCost}{dB_{<2>}} = [(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})] \times 1$

$\frac{dCost}{dB_{<2>}} = (\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})$


In the First Hidden Layer: $(l=1)$

**Assume Sigmoid as Activation Function

The Gradients of $A_{<1>}$ and $Z_{<1>}$ are:

$\frac{dCost}{dA_{<1>}} = \frac{dCost}{d\hat{Y}} \times \frac{d\hat{Y}}{dZ_{<3>}} \times \frac{dZ_{<3>}}{dA_{<2>}} \times \frac{dA_{<2>}}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dA_{<1>}}$

$\frac{dCost}{dA_{<1>}} = \frac{dCost}{dZ_{<2>}} \times \frac{dZ_{<2>}}{dA_{<1>}}$

$\frac{dCost}{dA_{<1>}} = [(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} \times W_{<2>}$

$\frac{dCost}{dA_{<1>}} = [(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} W_{<2>}$

$\frac{dA_{<1>}}{dZ_{<1>}} = A_{<1>}(1 - A_{<1>})$

Therefore:

$\frac{dCost}{dZ_{<1>}} = \frac{dCost}{dA_{<1>}} \times \frac{dA_{<1>}}{dZ_{<1>}}$

$= [(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} W_{<2>} \times A_{<1>}(1 - A_{<1>})$ (Element-Wise)

The Gradients of the Weights and Biases are:

$\frac{dZ_{<1>}}{dW_{<1>}} = X$

$\frac{dZ_{<1>}}{dB_{<1>}} = 1$

And:

$\frac{dCost}{dW_{<1>}} = \frac{dCost}{dZ_{<1>}} \times \frac{dZ_{<1>}}{dW_{<1>}}$

$\frac{dCost}{dB_{<1>}} = \frac{dCost}{dZ_{<1>}} \times \frac{dZ_{<1>}}{dB_{<1>}}$

Therefore:

$\frac{dCost}{dW_{<1>}} = [[(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} W_{<2>} \times A_{<1>}(1 - A_{<1>})] \times X^{T}$ (n_H1, m) x (m, n_In)

$\frac{dCost}{dW_{<1>}} = [[(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} W_{<2>} \times A_{<1>}(1 - A_{<1>})] X^{T}$ (n_H1, n_In)


$\frac{dCost}{dB_{<1>}} = [[(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} W_{<2>} \times A_{<1>}(1 - A_{<1>})] \times 1$

$\frac{dCost}{dB_{<1>}} = [[(\hat{Y} - Y)^{T} W_{<3>} \times A_{<2>}(1 - A_{<2>})]^{T} W_{<2>} \times A_{<1>}(1 - A_{<1>})]$


Note that:

$\large \frac{dCost}{dB_{<l>}} = dZ_{<l>}$

Also, we do not expand out the $A$s and $\hat{Y}$ as we will cache these values from the Forward Pass.


Backpropagation in Neural Networks

We notice that the Backpropagation of Gradients in a Neural Network works very similarly to that of Linear/Logistic Regressions, except that we have multiple layers and we are stacking the Chain Rule Continuously.

Once Gradients have been passed back through Backpropagation, we can update all the Model Parameters at once with Gradient Descent.


Vanishing & Exploding Gradients

As gradients are continuously multiplied in the backward pass due to the Chain Rule, Neural Networks can suffer from Vanishing/Exploding Gradients as the Network gets Extremely Deep.


4) Activation Functions

return to top

Sigmoid

Softmax

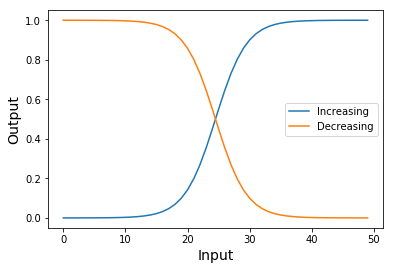
Tanh (Hyperbolic Tangent)

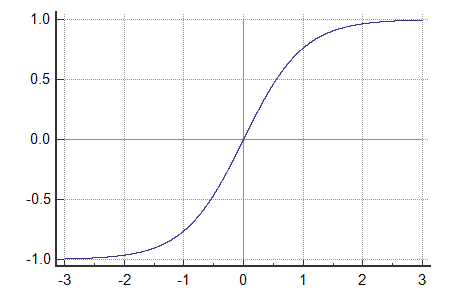
ReLU (Rectified Linear Unit)

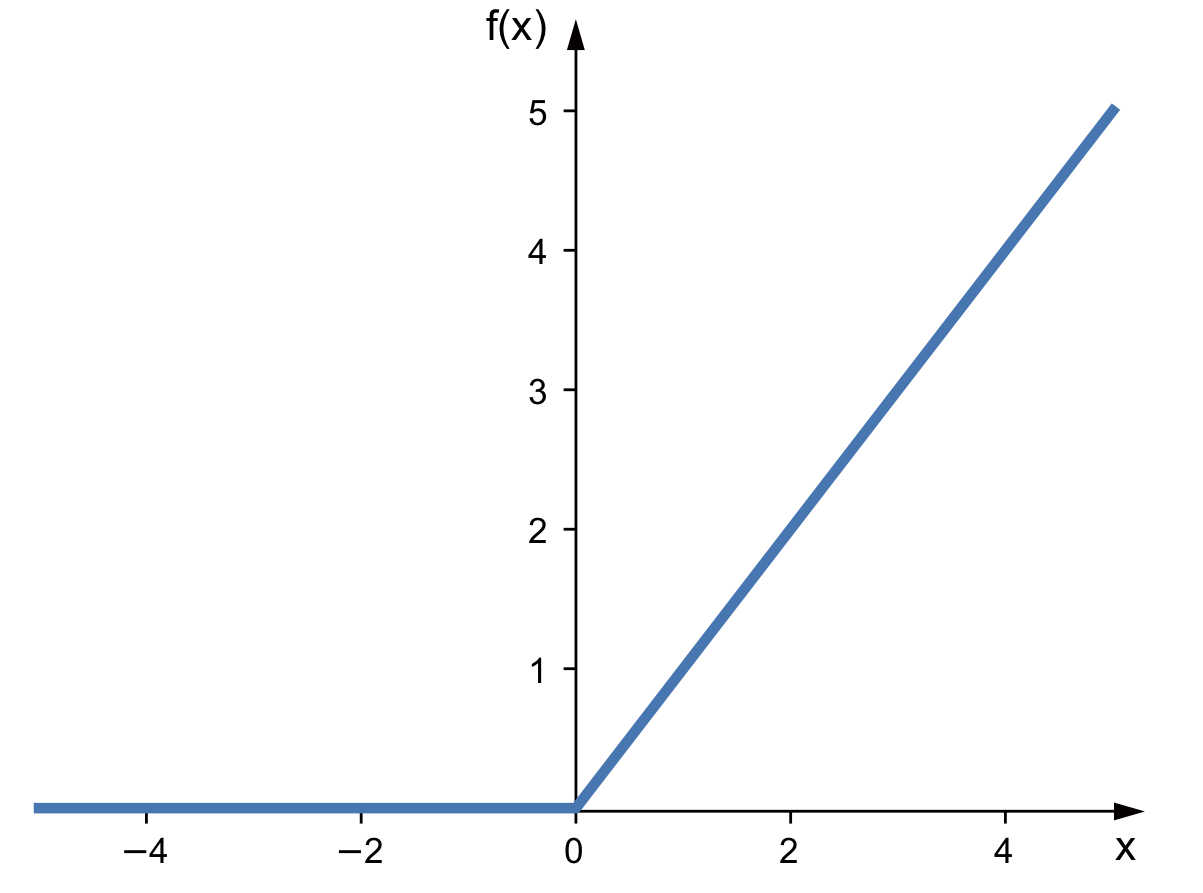
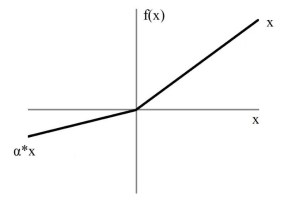
Leaky ReLU (Leaky Rectified Linear Unit)



5) Implementing a Neural Network

return to top

Iris Dataset Example

In [2]:
iris = datasets.load_iris()
In [3]:
iris.keys()
Out[3]:
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])

Define Num Features (n_F) and Num Classes(n_C)

In [4]:
n_F = len(iris['feature_names'])
n_C = len(iris['target_names'])

Shape of X and Y

In [5]:
iris['data'].shape, iris['target'].shape
Out[5]:
((150, 4), (150,))


Visualize Dataset in DataFrame

In [6]:
pd.DataFrame(iris['data'], columns=iris['feature_names']).head()
Out[6]:
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
In [7]:
iris.target_names
Out[7]:
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')


In [8]:
X = iris['data'].T
Y_class = iris['target']
In [9]:
X.shape, Y_class.shape
Out[9]:
((4, 150), (150,))


One-Hot Encode Labels

In [10]:
def one_hot(array, num_classes):
    new_array = np.zeros((len(array), num_classes))
    for i, val in enumerate(array):
        new_array[i, val] = 1
    return new_array
In [11]:
Y = one_hot(Y_class, n_C).T
In [12]:
Y.shape
Out[12]:
(3, 150)


Shuffle Data

In [13]:
indices = np.arange(iris['target'].shape[0])
np.random.shuffle(indices)
In [14]:
X = X[:,indices]
Y = Y[:,indices]
Y_class = Y_class[indices]


Train Test Split

In [15]:
split_ratio = 0.2
split = int(Y.shape[1] * split_ratio)

X_train = X[:, split:]
X_val = X[:, :split]
Y_train = Y[:, split:]
Y_val = Y[:, :split]
Y_class_train = Y_class[split:]
Y_class_val = Y_class[:split]
In [16]:
X_train.shape, X_val.shape
Out[16]:
((4, 120), (4, 30))


Instantiate Weights and Biases

In [17]:
w1 = np.random.randn(16, n_F)
w2 = np.random.randn(32, 16)
w3 = np.random.randn(n_C, 32)
In [18]:
b1 = np.random.randn(16, 1)
b2 = np.random.randn(32, 1)
b3 = np.random.randn(3, 1)
In [19]:
params = np.array([[b1, w1], 
                   [b2, w2], 
                   [b3, w3]])
In [20]:
params.shape
Out[20]:
(3, 2)

Define Model

In [21]:
from scipy.special import softmax
In [22]:
def model(params, X):
    Z1 = params[0,0] + np.dot(params[0,1], X) 
    A1 = np.maximum(Z1, 0) # ReLU
    Z2 = params[1,0] + np.dot(params[1,1], A1)
    A2 = np.maximum(Z2, 0) # ReLU
    Z3 = params[2,0] + np.dot(params[2,1], A2)
    y_hat = softmax(Z3, 0) # Softmax
    cache = {
        'Z1': Z1,
        'A1': A1,
        'Z2': Z2,
        'A2': A2,
        'Z3': Z3
    }
    return y_hat, cache

Test the Model to Check the Shape of the Output - Expected: C x M

In [23]:
y_hat, cache = model(params, X)
print(y_hat.shape)
print(cache.keys())

(3, 150)
dict_keys(['Z1', 'A1', 'Z2', 'A2', 'Z3'])


Define Cost Function (Cross Entropy Loss)

In [24]:
def cost(prediction, Y, epsilon=1e-10):
    error = np.sum((Y * np.log(prediction + epsilon)) + ((1 - Y) * np.log(1 - prediction + epsilon)), -1)/Y.shape[1]
    return - np.sum(error)


Define Training Algorithm

In [25]:
def train(X, Y, params, epochs=1, learning_rate=3e-6, iterations=1):
    
    for epoch in range(epochs):
        start = time.time()
        for iteration in range(iterations):
            
            # Forward Pass
            pred, cache = model(params, X)

            # Calculate Loss
            loss = cost(pred, Y)

            # Calculate Gradients (Backpropagation)

            # Layer 3
            dZ3 = pred - Y # c x m
            dw3 = np.dot(dZ3, cache['A2'].T) / dZ3.shape[1] # c x h2
            db3 = np.sum(dZ3, -1, keepdims=True) / dZ3.shape[1] # c x 1
            
            # Layer 2
            dA2 = np.dot(dZ3.T, params[2,1]).T # h2 x m
            dZ2 = dA2 * (cache['Z2'] > 0) # h2 x m
            dw2 = np.dot(dZ2, cache['A1'].T) / dZ2.shape[1] # h2 x h1
            db2 = np.sum(dZ2, -1, keepdims=True) / dZ2.shape[1] # h2 x 1
            
            # Layer 1
            dA1 = np.dot(dZ2.T, params[1,1]).T # h1 x m
            dZ1 = dA1 * (cache['Z1'] > 0) # h1 x m
            dw1 = np.dot(dZ1, X.T) / dZ1.shape[1] # h1 x I
            db1 = np.sum(dZ1, -1, keepdims=True) / dZ1.shape[1] # h1 x 1

            gradients = np.array([[db1, dw1], [db2, dw2], [db3, dw3]])   
            
            # Update Parameters (Gradient-Descent)
            params = params - (learning_rate * gradients)
            
            # Calculate Accuracy
            class_pred = np.argmax(pred, 0)
            class_y = np.argmax(Y, 0)

            acc = (class_pred == class_y).sum() / Y.shape[1]
        
        print('Epoch {}:'.format(epoch+1))
        print('Loss: {:.2f} | Accuracy: {:.2f}%\nTime Taken: {:.2f}s\n'.format(loss, acc*100, time.time()-start))
        
    return params
In [26]:
def predict(X, Y, params):
    # Forward Pass
    pred, _ = model(params, X)
    
    # Calculate Accuracy
    class_pred = np.argmax(pred, 0)
    class_y = np.argmax(Y, 0)
    acc = np.sum(class_pred == class_y)/Y.shape[1]
    
    return acc, pred


Time to train the Model

In [27]:
params = train(X_train, Y_train, params, epochs=20, iterations=5000)

Epoch 1:
Loss: 9.90 | Accuracy: 37.50%
Time Taken: 1.81s

Epoch 2:
Loss: 3.40 | Accuracy: 40.00%
Time Taken: 1.94s

Epoch 3:
Loss: 1.08 | Accuracy: 76.67%
Time Taken: 1.94s

Epoch 4:
Loss: 0.76 | Accuracy: 84.17%
Time Taken: 1.90s

Epoch 5:
Loss: 0.61 | Accuracy: 86.67%
Time Taken: 1.85s

Epoch 6:
Loss: 0.49 | Accuracy: 89.17%
Time Taken: 2.00s

Epoch 7:
Loss: 0.43 | Accuracy: 90.83%
Time Taken: 1.88s

Epoch 8:
Loss: 0.40 | Accuracy: 92.50%
Time Taken: 1.95s

Epoch 9:
Loss: 0.37 | Accuracy: 93.33%
Time Taken: 1.90s

Epoch 10:
Loss: 0.35 | Accuracy: 93.33%
Time Taken: 1.62s

Epoch 11:
Loss: 0.33 | Accuracy: 94.17%
Time Taken: 1.77s

Epoch 12:
Loss: 0.32 | Accuracy: 94.17%
Time Taken: 1.70s

Epoch 13:
Loss: 0.30 | Accuracy: 95.00%
Time Taken: 1.82s

Epoch 14:
Loss: 0.29 | Accuracy: 95.00%
Time Taken: 1.84s

Epoch 15:
Loss: 0.28 | Accuracy: 95.00%
Time Taken: 1.88s

Epoch 16:
Loss: 0.27 | Accuracy: 95.00%
Time Taken: 1.83s

Epoch 17:
Loss: 0.26 | Accuracy: 95.00%
Time Taken: 1.83s

Epoch 18:
Loss: 0.25 | Accuracy: 95.00%
Time Taken: 1.80s

Epoch 19:
Loss: 0.25 | Accuracy: 95.00%
Time Taken: 1.82s

Epoch 20:
Loss: 0.24 | Accuracy: 95.00%
Time Taken: 1.89s


In [28]:
acc, _ = predict(X_val, Y_val, params)

print('Accuracy of Prediction on Validation Data: {:.2f}%'.format(acc*100))

Accuracy of Prediction on Validation Data: 96.67%


Wine Dataset Example

In [29]:
wine = datasets.load_wine()
In [30]:
wine.keys()
Out[30]:
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])

Visualize Dataset in DataFrame

In [31]:
df = pd.DataFrame(wine['data'], columns=wine['feature_names'])
df.head()
Out[31]:
alcohol malic_acid ash alcalinity_of_ash magnesium total_phenols flavanoids nonflavanoid_phenols proanthocyanins color_intensity hue od280/od315_of_diluted_wines proline
0 14.23 1.71 2.43 15.6 127.0 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065.0
1 13.20 1.78 2.14 11.2 100.0 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050.0
2 13.16 2.36 2.67 18.6 101.0 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185.0
3 14.37 1.95 2.50 16.8 113.0 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480.0
4 13.24 2.59 2.87 21.0 118.0 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735.0
In [32]:
wine['target_names']
Out[32]:
array(['class_0', 'class_1', 'class_2'], dtype='<U7')

Copying Data Size and Data into Variables

In [33]:
n_F = len(wine['feature_names'])
n_C = len(wine['target_names'])
In [34]:
X = wine['data'].T
Y_class = wine['target']
Y = one_hot(Y_class, n_C).T

X.shape, Y_class.shape, Y.shape
Out[34]:
((13, 178), (178,), (3, 178))

Shuffle Data

In [35]:
indices = np.arange(wine['target'].shape[0])
np.random.shuffle(indices)

X = X[:,indices]
Y = Y[:,indices]
Y_class = Y_class[indices]

Train Test Split

In [36]:
split_ratio = 0.2
split = int(Y.shape[1] * split_ratio)

X_train = X[:, split:]
X_val = X[:, :split]
Y_train = Y[:, split:]
Y_val = Y[:, :split]
Y_class_train = Y_class[split:]
Y_class_val = Y_class[:split]
In [37]:
X_train.shape, X_val.shape
Out[37]:
((13, 143), (13, 35))

Instantiate Weights and Biases

In [38]:
w1 = np.random.randn(16, n_F)
w2 = np.random.randn(32, 16)
w3 = np.random.randn(n_C, 32)
In [39]:
b1 = np.random.randn(16, 1)
b2 = np.random.randn(32, 1)
b3 = np.random.randn(3, 1)
In [40]:
params = np.array([[b1, w1], 
                   [b2, w2], 
                   [b3, w3]])
In [41]:
params.shape
Out[41]:
(3, 2)

Train the Model

In [42]:
params = train(X_train, Y_train, params, epochs=20, iterations=5000, learning_rate=1e-6)

Epoch 1:
Loss: 16.10 | Accuracy: 57.34%
Time Taken: 2.22s

Epoch 2:
Loss: 15.12 | Accuracy: 60.14%
Time Taken: 2.12s

Epoch 3:
Loss: 13.81 | Accuracy: 61.54%
Time Taken: 2.09s

Epoch 4:
Loss: 13.10 | Accuracy: 61.54%
Time Taken: 1.98s

Epoch 5:
Loss: 10.97 | Accuracy: 67.83%
Time Taken: 2.02s

Epoch 6:
Loss: 10.30 | Accuracy: 69.23%
Time Taken: 2.13s

Epoch 7:
Loss: 9.19 | Accuracy: 69.23%
Time Taken: 2.08s

Epoch 8:
Loss: 7.95 | Accuracy: 71.33%
Time Taken: 2.00s

Epoch 9:
Loss: 5.09 | Accuracy: 81.12%
Time Taken: 1.90s

Epoch 10:
Loss: 5.29 | Accuracy: 78.32%
Time Taken: 2.02s

Epoch 11:
Loss: 5.20 | Accuracy: 78.32%
Time Taken: 2.25s

Epoch 12:
Loss: 5.04 | Accuracy: 79.72%
Time Taken: 2.22s

Epoch 13:
Loss: 4.87 | Accuracy: 81.12%
Time Taken: 2.25s

Epoch 14:
Loss: 4.64 | Accuracy: 81.82%
Time Taken: 2.11s

Epoch 15:
Loss: 4.38 | Accuracy: 81.82%
Time Taken: 1.81s

Epoch 16:
Loss: 4.11 | Accuracy: 82.52%
Time Taken: 1.95s

Epoch 17:
Loss: 3.75 | Accuracy: 82.52%
Time Taken: 2.07s

Epoch 18:
Loss: 3.18 | Accuracy: 84.62%
Time Taken: 1.91s

Epoch 19:
Loss: 1.94 | Accuracy: 87.41%
Time Taken: 2.06s

Epoch 20:
Loss: 1.78 | Accuracy: 88.11%
Time Taken: 1.95s


In [43]:
acc, _ = predict(X_val, Y_val, params)

print('Accuracy of Prediction on Validation Data: {:.2f}%'.format(acc*100))

Accuracy of Prediction on Validation Data: 80.00%




Previous: Next: