Machine Learning Programming Workshop

2.3 Multi-Class Classification with Logistic Regression

Prepared By: Cheong Shiu Hong (FTFNCE)


Contents


In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


1) Intuition Behind Multi-Class Logistic Regression

return to top

Instead of Classifying Cancer or No Cancer, what if we had Multiple Classes?

E.g. Classifying if a Sample is a Cat, Dog, Rat, or a Snake


Recap - Linear Regression


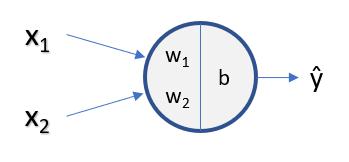
Recap - Binary Logistic Regression


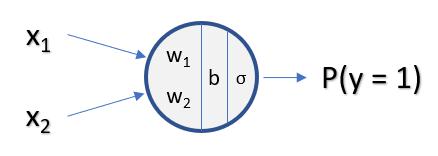
Multi-Class Logistic Regression

In Multi-Class Logistic Regression, the Ouptut of the Model will be a Vector instead of a Scalar Value

Each Number in the Vector Represents the Probability of each Sample being in that Class

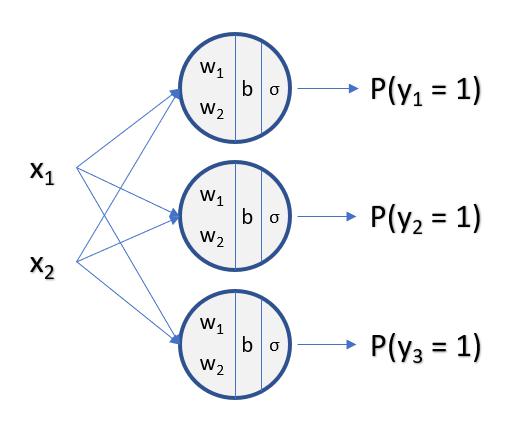
In the above scenerio of 3 Classes, the Output of the Model will be a Vector of 3 Values:

$\left[ {\begin{array}{c} P(y_{1} = 1) \\ P(y_{2} = 1) \\ P(y_{3} = 1) \end{array} } \right] $


To Output a Vector of 3 Values, We Need Three Seperate Calculations (Nodes) for Each Value

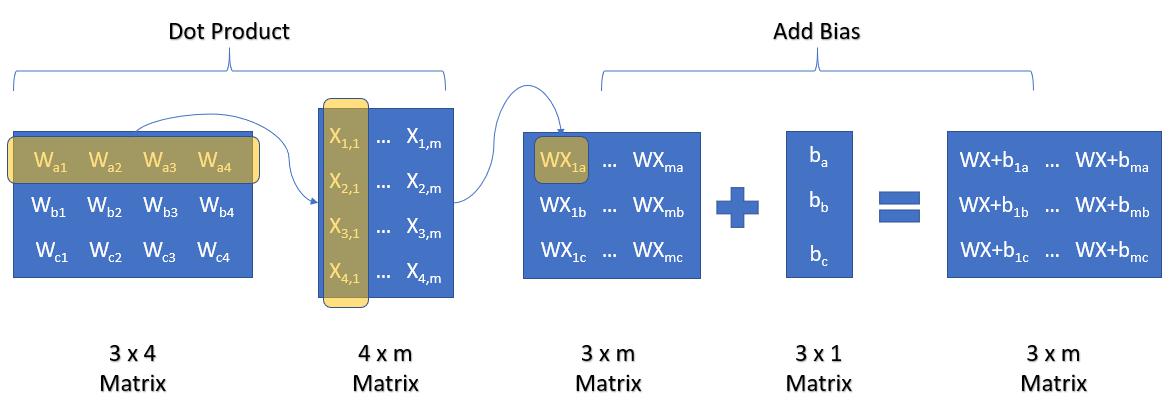
Weight Matrix:

The Weight Matrix Needs to be a (3 x 4) Matrix, or Number of Outputs (n_C) by Number of Inputs (n_F).

The Number of Rows is Number of Classes, and Number of Columns is Number of Features.


Bias Matrix:

Our Bias Matrix Needs to be a (3, 1) Matrix, or Number of Outputs (n_C) by 1.

The Number of Rows is Number of Classes, and Number of Columns is 1.


Question: Can the Sample be a Dog, a Cat, a Rat, and a Snake all at the Same Time?

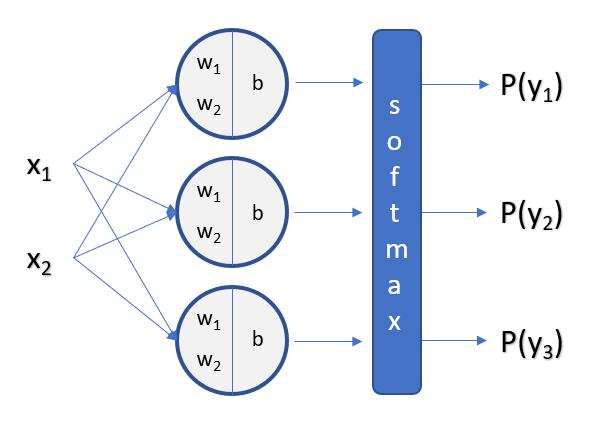
For Non-Inclusive (Exclusive) classes, We will use Softmax as our Activation Function instead of Sigmoid.


What is Softmax?

Hardmax is taking the Maximum Value of an Array and Outputting the Maximum as '1', while the rest are '0'.

$Hardmax(\left[ {\begin{array}{c} 0.1 \\ 1.2 \\ 0.5 \end{array} } \right])$ = $\left[ {\begin{array}{c} 0 \\ 1 \\ 0 \end{array} } \right]$

Softmax on the other hand, takes a 'Softer' Approach of Spreading the Values out on a Scale similar to Sigmoid.

The Highest Value will be set to a Value Closer to 1, while the Other Lower Values will be set to a Lower Value.

The Sum of All Values in the Vector for a Single Sample will add up to '1' with the below Formula:

$\sigma(z_{j}) = \frac{e^{z_{j}}}{\sum\limits^{C}_{i=1}e^{z_{i}}}$

$\sigma(Z) = \left[ {\begin{array}{c} \frac{e^{z_{1}}}{e^{z_{1}} + e^{z_{2}} + e^{z_{3}}} \\ \frac{e^{z_{2}}}{e^{z_{1}} + e^{z_{2}} + e^{z_{3}}} \\ \frac{e^{z_{3}}}{e^{z_{1}} + e^{z_{2}} + e^{z_{3}}} \end{array} } \right]$

Note that the Same Input Value might not always Output the Same Value, as the Output is Dependent on the other Input Values.


Define the Softmax Function

In [2]:
def softmax(array):
    return np.exp(array) / np.sum(np.exp(array), -1, keepdims=True)


Visualize what Softmax Does to a 2-Class Dataset

In [3]:
a = np.arange(50)/5
b = a[::-1]

c = np.vstack([a,b]).T

pd.DataFrame(c, columns=['Increasing', 'Decreasing'])
Out[3]:
Increasing Decreasing
0 0.0 9.8
1 0.2 9.6
2 0.4 9.4
3 0.6 9.2
4 0.8 9.0
5 1.0 8.8
6 1.2 8.6
7 1.4 8.4
8 1.6 8.2
9 1.8 8.0
10 2.0 7.8
11 2.2 7.6
12 2.4 7.4
13 2.6 7.2
14 2.8 7.0
15 3.0 6.8
16 3.2 6.6
17 3.4 6.4
18 3.6 6.2
19 3.8 6.0
20 4.0 5.8
21 4.2 5.6
22 4.4 5.4
23 4.6 5.2
24 4.8 5.0
25 5.0 4.8
26 5.2 4.6
27 5.4 4.4
28 5.6 4.2
29 5.8 4.0
30 6.0 3.8
31 6.2 3.6
32 6.4 3.4
33 6.6 3.2
34 6.8 3.0
35 7.0 2.8
36 7.2 2.6
37 7.4 2.4
38 7.6 2.2
39 7.8 2.0
40 8.0 1.8
41 8.2 1.6
42 8.4 1.4
43 8.6 1.2
44 8.8 1.0
45 9.0 0.8
46 9.2 0.6
47 9.4 0.4
48 9.6 0.2
49 9.8 0.0
In [4]:
plt.plot(softmax(c)[:,0], label='Increasing');
plt.plot(softmax(c)[:,1], label='Decreasing');
plt.xlabel('Input', fontsize=14), plt.ylabel('Output', fontsize=14)
plt.legend();


2) Multi-Class Logistic Regression with Iris Dataset

return to top

Import Iris Dataset from Sci-Kit Learn Library

In [5]:
import sklearn.datasets as datasets
import time # To Track Time
In [6]:
iris = datasets.load_iris()

Let's Check Out the Dataset

In [7]:
iris.keys()
Out[7]:
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
In [8]:
print("Feature Names:\n", iris['feature_names'], "\n\nLabel Names:\n", iris['target_names'])

Feature Names:
 ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] 

Label Names:
 ['setosa' 'versicolor' 'virginica']

Define Num Features (n_F) and Num Classes(n_C)

In [9]:
n_F = len(iris['feature_names'])
n_C = len(iris['target_names'])

Shape of X and Y

In [10]:
iris['data'].shape, iris['target'].shape
Out[10]:
((150, 4), (150,))
In [11]:
df = pd.DataFrame(iris['data'], columns=iris['feature_names'])
df.head()
Out[11]:
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
In [12]:
X = iris['data'].T
Y_class = iris['target']
In [13]:
X.shape, Y_class.shape
Out[13]:
((4, 150), (150,))


One-Hot Encode Labels

In [14]:
def one_hot(array, num_classes):
    new_array = np.zeros((len(array), num_classes))
    for i, val in enumerate(array):
        new_array[i, val] = 1
    return new_array
In [15]:
Y = one_hot(Y_class, n_C).T
In [16]:
Y.shape
Out[16]:
(3, 150)


Shuffle Data

In [17]:
indices = np.arange(iris['target'].shape[0])
np.random.shuffle(indices)
In [18]:
indices
Out[18]:
array([  1,  70, 107, 149,  76,  75,  15,  67, 130,  74, 129,  93, 140,
        64,  44,  54,  27,   2, 101,  87,  43,   5,  39,  79, 120,  20,
        33,   6,   4,  69,  10, 102,  73,  34,  63, 116,  47,   7,  29,
        53, 106, 104,  94,  24, 121,  30, 112,  58, 131,  60, 132, 115,
       108, 136, 127,  59,  41, 143, 100, 119, 109,   9, 134, 148, 122,
        28,  55,  56, 144,  51,  19,  36,  95,  91,  88,  72, 142, 118,
        78,  99, 114,  89,   3, 126,  86,  83,  61,  46, 105,  81,  97,
       117,  57,  26,  80,  42,  92, 110, 133,  17,  90, 135, 111, 124,
       141, 145,  96,  71, 113,  49,  35,  45,  21,  32, 128,  68, 125,
        25,  37,  98, 147,   0, 137,  82,  66,  31,  62, 138, 123,  77,
        22,  18, 139,  48,  85,  50,  38,  23,  84,   8,  14,  13,  11,
       103, 146,  65,  16,  40,  12,  52])
In [19]:
X = X[:,indices]
Y = Y[:,indices]
Y_class = Y_class[indices]


Train Test Split

In [20]:
split_ratio = 0.2
split = int(Y.shape[1] * split_ratio)

X_train = X[:, split:]
X_val = X[:, :split]
Y_train = Y[:, split:]
Y_val = Y[:, :split]
Y_class_train = Y_class[split:]
Y_class_val = Y_class[:split]


Initialize Weights and Biases

Weights (C x F)

In [21]:
weights = np.random.randn(n_C, n_F) # Num Classes x Num Features
In [22]:
weights
Out[22]:
array([[ 0.91057411, -1.73159604,  0.25916453,  0.65316311],
       [-0.19227925, -0.28523107, -0.78849773,  0.02460387],
       [-0.15662074, -0.57448763, -1.70533646, -0.71892338]])

Biases (C x 1)

In [23]:
biases = np.zeros((n_C, 1))
In [24]:
biases
Out[24]:
array([[0.],
       [0.],
       [0.]])


Define Model

In [25]:
# Activation Function 
def softmax(x):
    return np.exp(x)/sum(np.exp(x))
In [26]:
# Model
def model(biases, weights, X):
    return softmax(biases + np.dot(weights, X))

Test the Model to Check the Shape of the Output - Expected: C x M

In [27]:
model(biases, weights, X_train).shape
Out[27]:
(3, 120)


Define Cost Function

In [28]:
def cost(prediction, Y, epsilon=1e-10):
    error = np.sum((Y * np.log(prediction + epsilon)) + ((1 - Y) * np.log(1 - prediction + epsilon)), -1)/Y.shape[1]
    return - np.sum(error)


Define Training Algorithm

In [29]:
def train(X, Y, biases, weights, epochs=1, learning_rate=1e-2, iterations=1):
    
    for epoch in range(epochs):
        start = time.time()
        for iteration in range(iterations):
            # Forward Pass
            pred = model(biases, weights, X)

            # Calculate Loss
            loss = cost(pred, Y)

            # Calculate Gradients
            db = np.sum((pred - Y), -1, keepdims=True) / Y.shape[1]
            dw = np.dot((pred - Y), X.T) / Y.shape[1]

            # Calculate Accuracy
            class_pred = np.argmax(pred, 0)
            class_y = np.argmax(Y, 0)
            acc = np.sum(class_pred == class_y)/Y.shape[1]

            # Update Biases and Weights
            biases -= (learning_rate * db)
            weights -= (learning_rate * dw)
        
        print('Epoch {}:'.format(epoch+1))
        print('Loss: {:.2f} | Accuracy: {:.2f}%\nTime Taken: {:.2f}s\n'.format(loss, acc*100, time.time()-start))
        
    return biases, weights


Define Function for Predicting

In [30]:
def predict(X, Y, biases, weights):
    # Forward Pass
    pred = model(biases, weights, X)
    
    # Calculate Accuracy
    class_pred = np.argmax(pred, 0)
    class_y = np.argmax(Y, 0)
    acc = np.sum(class_pred == class_y)/Y.shape[1]
    
    return acc, pred


Training The Parameters for 20 x 100 Iterations

In [31]:
biases, weights = train(X_train, Y_train, biases, weights, epochs=20, iterations=100)

Epoch 1:
Loss: 2.48 | Accuracy: 13.33%
Time Taken: 0.01s

Epoch 2:
Loss: 1.56 | Accuracy: 66.67%
Time Taken: 0.01s

Epoch 3:
Loss: 1.23 | Accuracy: 67.50%
Time Taken: 0.01s

Epoch 4:
Loss: 1.09 | Accuracy: 70.83%
Time Taken: 0.01s

Epoch 5:
Loss: 1.00 | Accuracy: 75.83%
Time Taken: 0.01s

Epoch 6:
Loss: 0.94 | Accuracy: 83.33%
Time Taken: 0.01s

Epoch 7:
Loss: 0.89 | Accuracy: 89.17%
Time Taken: 0.01s

Epoch 8:
Loss: 0.85 | Accuracy: 90.00%
Time Taken: 0.01s

Epoch 9:
Loss: 0.81 | Accuracy: 92.50%
Time Taken: 0.02s

Epoch 10:
Loss: 0.78 | Accuracy: 94.17%
Time Taken: 0.01s

Epoch 11:
Loss: 0.75 | Accuracy: 95.00%
Time Taken: 0.01s

Epoch 12:
Loss: 0.73 | Accuracy: 95.83%
Time Taken: 0.02s

Epoch 13:
Loss: 0.70 | Accuracy: 95.83%
Time Taken: 0.02s

Epoch 14:
Loss: 0.68 | Accuracy: 96.67%
Time Taken: 0.01s

Epoch 15:
Loss: 0.66 | Accuracy: 96.67%
Time Taken: 0.01s

Epoch 16:
Loss: 0.64 | Accuracy: 96.67%
Time Taken: 0.01s

Epoch 17:
Loss: 0.63 | Accuracy: 96.67%
Time Taken: 0.02s

Epoch 18:
Loss: 0.61 | Accuracy: 96.67%
Time Taken: 0.01s

Epoch 19:
Loss: 0.60 | Accuracy: 96.67%
Time Taken: 0.01s

Epoch 20:
Loss: 0.58 | Accuracy: 96.67%
Time Taken: 0.01s
In [32]:
acc, _ = predict(X_val, Y_val, biases, weights)

print('Accuracy of Prediction on Validation Data: {:.2f}%'.format(acc*100))

Accuracy of Prediction on Validation Data: 96.67%


3) Multi-Class Logistic Regression with Sci-Kit Learn

return to top

Sci-Kit Learn is a Powerful Python Library that has Many Built-In Machine Learning Algorithms

Import Sklearn's Logistic Regression Object from sklearn.linear_model

In [33]:
from sklearn.linear_model import LogisticRegression


Instantiate the Logistic Regression Object

In [34]:
model = LogisticRegression(solver='liblinear', multi_class='ovr', verbose=1)


Fit Model to Data

In [35]:
model.fit(X_train.T, Y_class_train)

[LibLinear]
Out[35]:
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr',
          n_jobs=None, penalty='l2', random_state=None, solver='liblinear',
          tol=0.0001, verbose=1, warm_start=False)


Evaluate Score of Fitted Model

In [36]:
# Training Set
model.score(X_train.T, Y_class_train)
Out[36]:
0.9666666666666667
In [37]:
# Validation Set
model.score(X_val.T, Y_class_val)
Out[37]:
0.9333333333333333

Note: When passing Labels(Y) into Sci-kit Learn, one-hot encoding is not required


Evaluate Cross Entropy Loss of Fitted Model

In [38]:
skpred_t = model.predict_proba(X_train.T)
skpred_v = model.predict_proba(X_val.T)
skpred = model.predict_proba(X.T)

epsilon = 1e-10

# Cross Entropy Loss
train_loss = - np.mean((Y_train.T * np.log(skpred_t + epsilon)) + ((1-Y_train.T) * np.log(1-skpred_t + epsilon)))
val_loss = - np.mean((Y_val.T * np.log(skpred_v + epsilon)) + ((1-Y_val.T) * np.log(1-skpred_v + epsilon)))
total_loss = - np.mean((Y.T * np.log(skpred + epsilon)) + ((1-Y.T) * np.log(1-skpred + epsilon)))

print('Train Set Loss: {:.4f}'.format(train_loss))
print('Validation Set Loss: {:.4f}'.format(val_loss))
print('Total Loss: {:.4f}'.format(total_loss))

Train Set Loss: 0.2199
Validation Set Loss: 0.1911
Total Loss: 0.2141


What happens if we keep stacking layers?


4) Other Algorithms

return to top

Sci-kit Learn Documentation

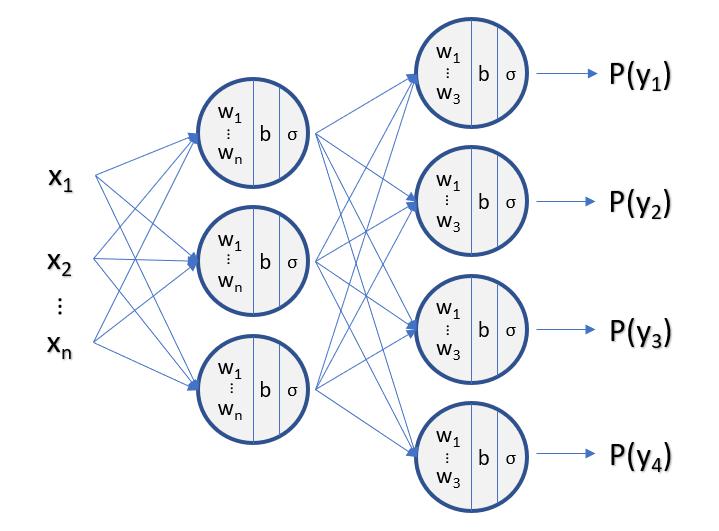
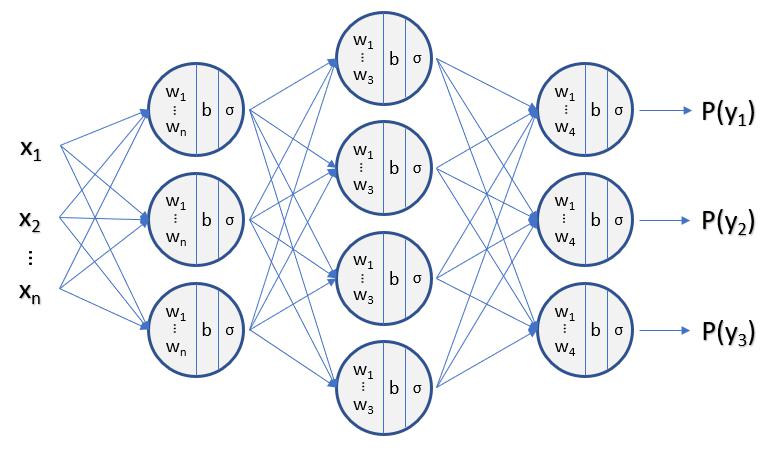
Naive Bayes

In [39]:
from sklearn.naive_bayes import GaussianNB
In [40]:
NB = GaussianNB()
In [41]:
NB.fit(X.T, Y_class)
Out[41]:
GaussianNB(priors=None, var_smoothing=1e-09)
In [42]:
NB.score(X.T, Y_class)
Out[42]:
0.96


Decision Trees

In [43]:
from sklearn.tree import DecisionTreeClassifier
In [44]:
dec_tree = DecisionTreeClassifier()
In [45]:
dec_tree.fit(X.T, Y_class)
Out[45]:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=None,
            splitter='best')
In [46]:
dec_tree.score(X.T, Y_class)
Out[46]:
1.0


Support Vector Machines

In [47]:
from sklearn.svm import SVC
In [48]:
SVM1 = SVC(kernel='linear')
SVM2 = SVC()
In [49]:
SVM1.fit(X.T, Y_class)
SVM2.fit(X.T, Y_class)

C:\Users\cheon\Anaconda3\lib\site-packages\sklearn\svm\base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
  "avoid this warning.", FutureWarning)
Out[49]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
  kernel='rbf', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
In [50]:
SVM1.score(X.T, Y_class), SVM2.score(X.T, Y_class)
Out[50]:
(0.9933333333333333, 0.9866666666666667)


Ensemble Algorithms

In [51]:
from sklearn.ensemble import RandomForestClassifier
In [52]:
RFC = RandomForestClassifier()
In [53]:
RFC.fit(X.T, Y_class)

C:\Users\cheon\Anaconda3\lib\site-packages\sklearn\ensemble\forest.py:246: FutureWarning: The default value of n_estimators will change from 10 in version 0.20 to 100 in 0.22.
  "10 in version 0.20 to 100 in 0.22.", FutureWarning)
Out[53]:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
            max_depth=None, max_features='auto', max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None,
            oob_score=False, random_state=None, verbose=0,
            warm_start=False)
In [54]:
RFC.score(X.T, Y_class)
Out[54]:
1.0


Neural Networks</h4>

In [55]:
from sklearn.neural_network import MLPClassifier
In [56]:
NN1 = MLPClassifier(max_iter=1000, hidden_layer_sizes=3)
NN2 = MLPClassifier(max_iter=1000, hidden_layer_sizes=100)
NN3 = MLPClassifier(max_iter=1000, hidden_layer_sizes=300)
In [57]:
NN1.fit(X.T, Y_class)
NN1.score(X.T, Y_class)

C:\Users\cheon\Anaconda3\lib\site-packages\sklearn\neural_network\multilayer_perceptron.py:562: ConvergenceWarning: Stochastic Optimizer: Maximum iterations (1000) reached and the optimization hasn't converged yet.
  % self.max_iter, ConvergenceWarning)
Out[57]:
0.6333333333333333
In [58]:
NN2.fit(X.T, Y_class)
NN2.score(X.T, Y_class)
Out[58]:
0.98
In [59]:
NN3.fit(X.T, Y_class)
NN3.score(X.T, Y_class)
Out[59]:
0.98
In [60]:
NN4 = MLPClassifier(max_iter=1000, hidden_layer_sizes=(25,50,25))
In [61]:
NN4.fit(X.T, Y_class)
NN4.score(X.T, Y_class)
Out[61]:
0.98




Previous: Next: